Heap : Heap을 만드는데 필요한 시간 복잡도
- CS/자료구조
- 2022. 4. 4.
Heap Build 시간복잡도는 O(NLogN)이 아니다!
얼마 전에 알게 된 사실이다. Heap Build에 필요한 시간복잡도는 O(nlogn)이 아니다. 바로 O(n)이다. 나는 당연히 Heapfy를 한번 하는데 필요한 시간 복잡도가 O(logn)이기 때문에 n개의 리스트를 Heap으로 만들면 당연히 O(nlogn)으로 이해를 하고 있었다. 그런데 실제로는 그것보다 더 적은 값으로 계산이 된다고 한다.
이곳(Time Complexity of building a heap - GeeksforGeeks)에 증명이 되어있었고, 그것을 내가 알아보기 쉽게.. 부족한 수학 머리로 간단히 정리해본다.

먼저 Heap Build 시간복잡도는 다음과 같은 식을 세울 수 있다. 여기서 n은 Array나 List의 최대 크기다. 그리고 h는 이 Array를 가지고 만들 수 있는 Heap의 높이다. 그런데 Sigma로 되어있고, h = 0부터 log(n)까지 h가 변한다고 한다.
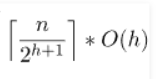
좀 더 쉽게 말해, 요 위의 식은 각 층에 있는 노드의 수에 해당 높이만큼 곱한다. 이렇게 되는 이유는 처음부터 Heap의 높이가 최종 만들어졌을 때의 높이가 되지 않는다. 예를 들어 n = 1 ~ 10까지 움직이기 때문에 처음에 높이는 0이 되고, 그 다음에는 1,2,3인 힙이 차례차례 만들어지기 때문이다. 따라서 위의 수식처럼 분절화 해서 만들 수 있다.

그리고 위의 수식을 설명하기 위한 한 가지 그림이 더 필요하다. h = 0인 값을 대입해보면, 좌변은 (7/ 2) = 4(올려서)가 된다. 즉, 해당 높이에 있는 Node의 갯수는 많아봐야 좌변만큼 있다는 것을 의미한다. 해당 Height에 Heap 구조를 형성하는데 총 좌변 만큼의 Node만큼 Heapfy를 해야하기 때문에 위와 같은 식이 나온 것이다.


위 수식은 다음과 같이 더해야 할 값을 무한대로 바꿀 수 있다. 왜냐하면 컴퓨팅에서는 무한히 많은 값들에 대해서 값을 구하기 때문에 log(n)으로 대변되는 Height 역시 충분히 무한할 수 있기 때문이다. 왼쪽에 있는 식만으로는 결론을 낼 수가 없다. 그래서 오른쪽의 식을 가지고 온다. (어디서 왔는지는 잘 모르겠다. 공학 수학할 때 배웠던 것 같은데..)

위의 식을 대입해줄 경우, Heap Build의 시간 복잡도는 O(n)으로 일반화 할 수 있다. 따라서, 기존에 내가 알고 있던 nlogn의 시간복잡도가 아니라, Heap Build는 O(n)이 된다.
'CS > 자료구조' 카테고리의 다른 글
| 자료구조 : 큐와 덱 (0) | 2021.10.04 |
|---|---|
| 정렬 알고리즘 정리 (0) | 2021.10.03 |
| Heap 구조 및 파이썬 구현 (0) | 2021.09.30 |
| 테이블과 해시 함수 (0) | 2021.09.26 |
| 세그먼트 트리의 Lazy Propagation + 파이썬 구현 (0) | 2021.09.22 |