백준 17071 숨바꼭질5 파이썬
- CS/BOJ
- 2022. 2. 21.
https://www.acmicpc.net/problem/17071
17071번: 숨바꼭질 5
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 500,000)에 있고, 동생은 점 K(0 ≤ K ≤ 500,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때
www.acmicpc.net
숨바꼭질5는 수빈이 뿐만 아니라 동생도 움직인다. 동생이 고정되어있을 때는 고정된 한점으로 이동하는 최단 경로를 찾기 때문에 쉽게 문제를 풀 수 있다. 그렇지만 이번에는 동생도 동적으로 움직인다. 그렇다면 여기서 고려해야할 부분은 예전에 방문했던 부분을 다시 방문하지 않아도 되냐는 것이다.
결론은 예전에 방문했던 부분을 다시 방문해야한다는 것이다. 이전에는 동생의 위치가 고정되어 있었기 때문에 최단 경로가 이미 정해져있었다. 그렇지만 이번에는 동생이 이동하기 때문에 그 순간의 동생의 위치로 가는 최단경로는 매번 바뀐다. 따라서 이전에 방문했던 곳이라도 최단 경로가 될 여지가 남아있다. 따라서 기본적인 BFS로는 풀 수 없다.
경우의 수가 굉장히 많기 때문에 이분탐색으로 줄일 수 있는지를 검토해봤다. 그렇지만 이 역시 정당하지 않다. 왜냐하면 동생과 수빈이가 10초에 만났다고 가정해보자. 11초, 12초, 13초, 14초에도 만날 수 있는 것이 반드시 보장되지 않는다. 왜냐하면 동생이 매 초 이동하는 거리와 수빈이가 이동하는 거리는 다르기 때문이다. 따라서 특정 범위의 최소값을 구하는 형식의 이분탐색으로 접근을 할 수 없다.
먼저 BFS로 (경계 조건을 풀고) 접근하면 당연한 이야기지만 TLE 혹은 메모리 초과가 난다. 왜냐하면 방문했던 위치에 계속 방문하기 때문에 큐에 무한정 많은 값이 들어가기 때문이다. 어떻게든 값을 줄여야하기 때문에 또 다른 방법이 있지 않을까 고민을 했다.
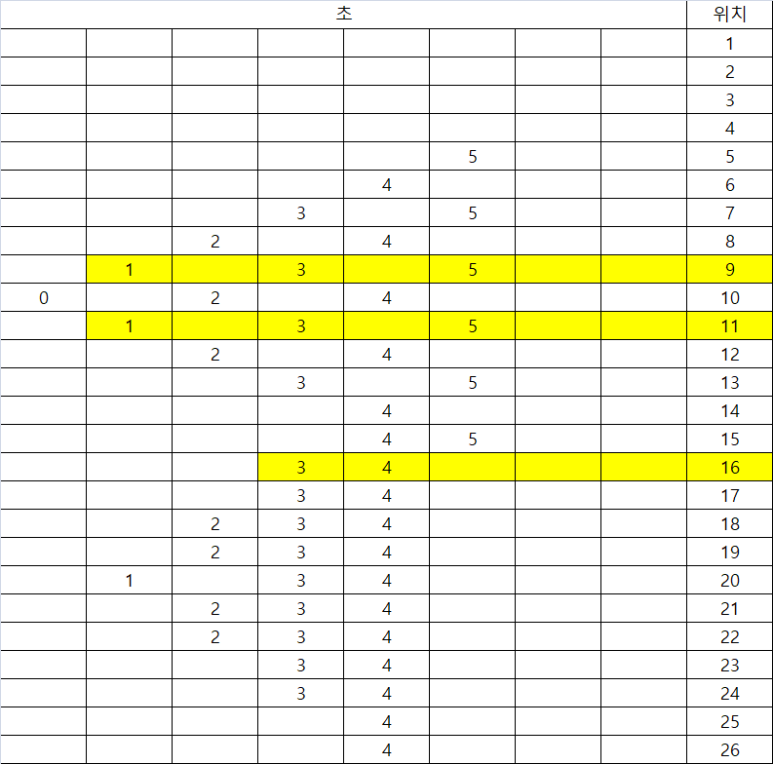
오른쪽은 좌표, 왼쪽은 매초 수빈이가 가능한 위치를 손수 노가다로 그렸다. 보니까 순간이동을 하는 경우에는 한번 도착하기만 하면 그 이후로는 항상 방문이 가능하다. 그렇지만 순간이동을 하지 않은 부분에서는 홀수 초에 도착하면 항상 홀수 초에 만났을 수 있는 것을 알 수 있다.
처음에는 그렇게 접근해서 1개의 배열로 현재 위치에 가장 빨리온 위치가 홀수/짝수냐에 따라 판별하는 방식으로 접근했다. 그렇지만 곧 틀린 것을 알게 되었다. 왜냐하면 홀수에서 이동한 곳도 *2이기 때문에 항상 짝수가 될 수 있기 때문이다. 즉, 홀수와 짝수 배열을 나누어 관리하면 문제가 없다는 것을 이해하게 되었다.
따라서 결론은 다음과 같다.
- 홀수초/짝수초 배열로 먼저 각 위치에 수빈이가 도착할 수 있는 최소 시간을 구한다.
- 동생이 이동하면서 각 초 + 위치마다 그 위치에 해당되는 시간을 확인한다.
- 동생이 도착한 시간이 수빈이가 도착한 시간보다 느리면, 항상 만날 수 있다.
- 3의 최소값을 구해서 출력하면 된다.
import sys
from collections import deque
def inner_function(now_posi, next_time, que, v ):
if now_posi + 1 <= 500000 and v[now_posi + 1] > next_time:
v[now_posi + 1] = next_time
que.append((now_posi + 1, next_time))
if now_posi - 1 >= 0 and v[now_posi - 1] > next_time:
v[now_posi - 1] = next_time
que.append((now_posi - 1, next_time))
if now_posi * 2 <= 500000 and v[now_posi * 2] > next_time:
v[now_posi * 2] = next_time
que.append((now_posi * 2, next_time))
return
def sol(n):
global ans
que = deque()
que.append((n,0))
if n % 2 == 0 :
v_even[n] = 0
else :
v_odd[n] = 0
while que :
now_posi, time = que.popleft()
next_time = time + 1
if next_time % 2 == 0 :
inner_function(now_posi, next_time, que, v_even)
else :
inner_function(now_posi, next_time, que, v_odd)
return
def sol2(k):
global ans
time = 0
while True:
k = k + time
if k > 500000 :
return
if time % 2 == 0 :
if v_even[k] <= time:
ans = time
return
elif time % 2 == 1:
if v_odd[k] <= time:
ans = time
return
time +=1
n,k = map(int,sys.stdin.readline().split())
v_odd = [9876543210 for _ in range(500000 + 1 )]
v_even = [9876543210 for _ in range(500000 + 1 )]
ans = 9876543210
if n == k :
print(0)
else :
myStr = sol(n)
sol2(k)
if ans == 9876543210 :
print(-1)
else:
print(ans)'CS > BOJ' 카테고리의 다른 글
| 백준 16920 확장게임 (0) | 2022.02.21 |
|---|---|
| 백준 22862 가장 긴 짝수 연속한 부분 수열 (large) (0) | 2022.02.21 |
| 백준 20922 겹치는 건 싫어 파이썬 (0) | 2022.02.21 |
| 백준 13913 숨바꼭질4 (0) | 2022.02.19 |
| 백준 13549 파이썬 (0) | 2022.02.19 |