누적합(Prefix)는 언제쓰지?
누적합은 특정 수열이 주어지고, 그 수열에서 특정 구간의 값을 구하라는 쿼리가 반복적으로 들어올 때 주로 사용하게 되는 개념이다. 예를 들어 길이 n의 수열이 주어졌을 때, [0, n-1] 구간의 합이 얼마인지를 확인하라는 반복적인 쿼리가 들어올 수 있다. 이 때, [0, n-1] 구간의 합을 확인하는데 필요한 시간복잡도는 O(N)이다.
이런 쿼리가 한번만 들어오면 크게 문제는 없지만, 대부분 이런 경우는 쿼리가 반복적으로 들어온다. 이 경우, 최악의 경우 주어진 쿼리를 다 처리하는데 필요한 시간복잡도는 O(N^2)이 된다. 이 시간복잡도를 O(N)으로 처리하기 위해 필요한 개념이 누적합이다.
수열에 주어진 정보의 각각 구간의 누적합을 찾아내고, 그 값을 배열로 관리한다. 그리고 그 배열로 필요한 영역의 정보를 빠르게 접근하겠다는 개념이다.
1차원 누적합
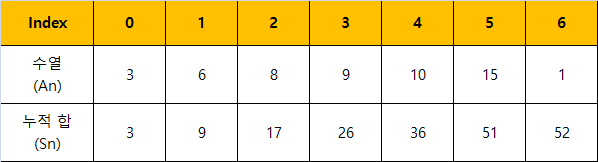
1차원 누적합은 위의 표로 간단히 나타낼 수 있다. Sn = (A1 + A2 + ... + An)으로 표현을 할 수 있다. 실제로 누적합을 구하는 배열을 관리할 때는 Sn = Sn-1 + An 점화식으로 표현하면 쉽게 구할 수 있다.
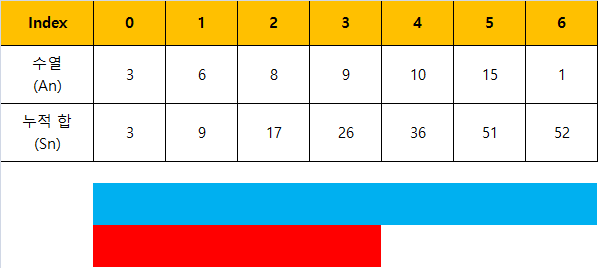
위의 이미지는 A4 ~ A6의 구간합을 구하는 것을 도식화한 그림이다. S6은 A1~A6까지의 합이고, 파란색 막대로 표현이 된다. S3은 A1~A3까지의 합이고 빨간색 막대로 표현이 된다. A4 ~ A6는 파란색 막대에서 빨간색 막대를 뺀 영역이다. A4~A6는 결국 S6 - S3으로 한 번에 구할 수 있다.
2차원 누적합

항상 1차원 배열에 대한 쿼리만 들어오면 좋겠지만, 2차원 배열이 들어오는 경우가 있다. 이 경우에는 1차원 누적합 개념에서 발전된 2차원 누적합 개념을 적용해야한다. 2차원 누적합에서 Sij는 A00 ~ Aij까지의 합을 구한 값으로 정의한다.
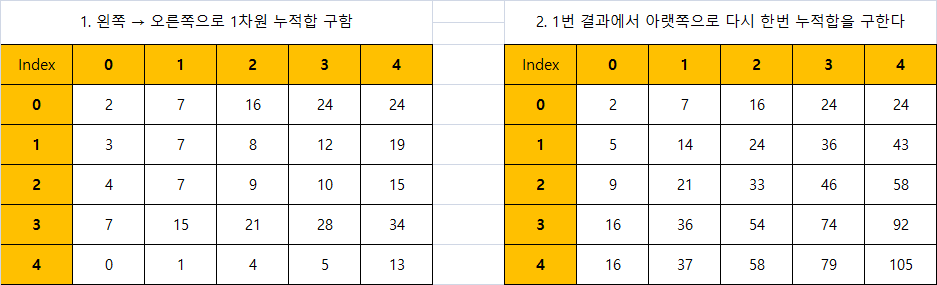
2차원 누적합을 구하기 위해서는 두 번의 쿼리 단계를 거쳐야 한다. 위의 이미지에서 확인이 가능하다. 먼저 왼쪽에서 오른쪽으로 1차원 누적합을 구한다. 구하면 왼쪽 테이블이 만들어진다. 왼쪽 테이블에서 세로 방향(위에서 아래 방향)으로 다시 한번 누적합을 구하게 되면 2차원 누적합을 온전히 표현하는 테이블이 만들어진다.
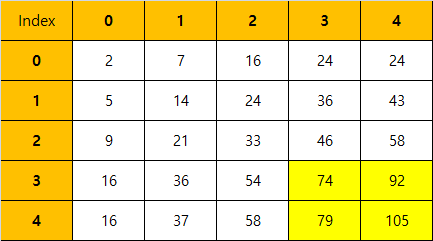
2차원 누적합 배열에서 노란색으로 표현된 영역의 값을 구한다고 가정해보자. 이 때는 어떻게 접근을 해야할까?
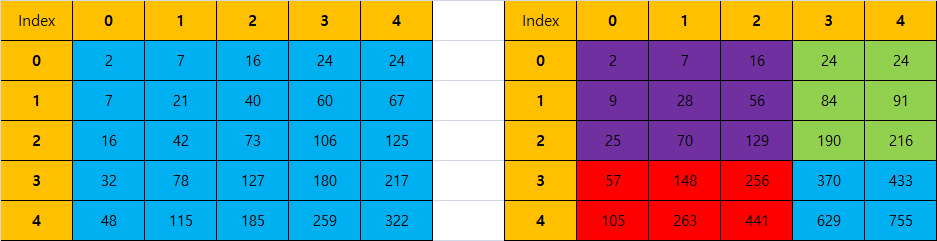
먼저 S44를 선택해준다. 왼쪽 그림의 파란색으로 표현이 가능하다. 그리고 파란색에서 빨간색으로 표현된 S42과 연두색으로 표현된 S24를 S44에서 빼주면 된다. 그런데 여기서 보라색 부분은 빨간색과 연두색 직사각형을 뺄 때 중복해서 빼진다. 이런 이유로 보라색 부분을 한번 더해주게 되면, 원하는 누적합을 구할 수 있다.
누적합의 한계
누적합은 반복적으로 누적합만 구하는 쿼리에 대해서는 빠르게 동작이 가능하다. 그렇지만 수열의 값이 변하는 경우에는 사용하기가 적절하지 않다. 수열의 값이 변할 때 마다 누적합 테이블을 다시 만들어야 하는데 1차원 테이블은 O(N), 2차원 테이블은 O(N^2)이 필요하기 때문이다.
누적합을 구해야 하는데, 구간의 요소가 자꾸 변하는 상황에서는 누적합보다는 누적합 세그먼트 트리를 구성하여 O(NlogN)으로 처리하는 것이 성능 개선에 중요한 역할을 한다.
'CS > 알고리즘' 카테고리의 다른 글
| Meet In The Middle 알고리즘 (0) | 2021.10.08 |
|---|---|
| 최소 스패닝 트리와 크루스칼 알고리즘 (0) | 2021.10.04 |
| 그리디 알고리즘 (0) | 2021.09.27 |
| 파이썬 알고리즘 필요 라이브러리 (0) | 2021.09.12 |
| 파이썬, Lower Bound 및 Upper Bound 구현 (0) | 2021.08.22 |